Asymptotic Notation

Common growth rates

(increasing order)

• \(\Theta(1)\)
• \(\Theta(\log n)\)
• \(\Theta(\sqrt{n})\)
• \(\Theta(n)\)
• \(\Theta(n^2)\)
• \(\Theta(n^c)\)
• \(\Theta(n^\sqrt{n} \log n)\) (best known algorithm for graph isomorphism)
• \(\Theta(c^{c(\log n)^{1/3}(\log \log n)^{2/3}})\) (factoring algorithm)
• \(\Theta(1.1^n)\)
• \(\Theta(2^n)\)
• \(\Theta(c^n)\)
• \(\Theta(n!)\)
• \(\Theta(c^n)\)

Loop analysis

e.g. 1

Using \(\Theta\)

• Loop on \(k\): \(\Theta(1)\)
  • number of iterations: \(j-i+1\)
  • Complexity is \(Theta(j-i+1)\)
• Loop on \(j\):
  • Complexity: \(\sum_{j=i}^n \Theta(j-i+1) = \Theta(i+2+...+n(n-i+1))\)
  • \(\Theta\left(\frac{(n-i+1)(n-i+2)}{2}\right)\)
  • \(\Theta(n^3)\)

Using separate upper and lower bounds: Modified loop structures

• Loop 1
  • \(i = 1, ..., \frac{n}{3}\)
  • \(j=\frac{2n}{3},...,n\)
  • \(k=\frac{2n}{3},...,n\)
  • \(\Omega(\frac{n}{3} \cdot \frac{n}{3} \cdot \frac{n}{3}) = \Omega(n^3)\)
• Loop 2
  • \(i=1,...,n\)
  • \(j=i+1,...,n\)
  • \(k=i,...,j\)
  • \(1 \le i \le k \le j \le n\)
• Loop 3
  • \(i=1,...,n\)
  • \(j=1,...,n\)
  • \(k=1,...,n\)
  • \(O(n^3)\)
• \(L1 \subseteq L2 \subseteq L3\)
• \(\Theta(n^3)\)

e.g. 2

• \(j = i, \frac{i}{2}, \frac{i}{4}, \frac{i}{8}, ..., 1\)
  • Number of iterations: \(\log_{2} i\)
  • \(\Theta(\log(1*2*3*...*n))\)
  • \(\Theta(\log(n!))\)
  • \(\Theta(n\log n)\)

Recurrence Relations

A formula expressing the general term \(a_n\) in terms of previous terms. Solving refers to finding a formula that is not recursive

Recursion tree method

e.g. for a recurrence relation:
\[T(n) = \begin{cases} aT\left(\frac{n}{b}\right) + cn, &n &gt 1\\ d, &\text{otherwise} \end{cases}\]

1. Start with one node tree having the value \(T(n)\)
2. Grow to \(a\) children. Each of these have values \(\frac{n}{b}\).
3. Repeat recursively until you reach \(T(1) = d\)

e.g. Mergesort

For the relation:
\[T(n) = \begin{cases} 2T\left(\frac{n}{2}\right) + cn, &n &gt 1 \text{ is a power of 2 }\\ d, n=1 \end{cases}\]

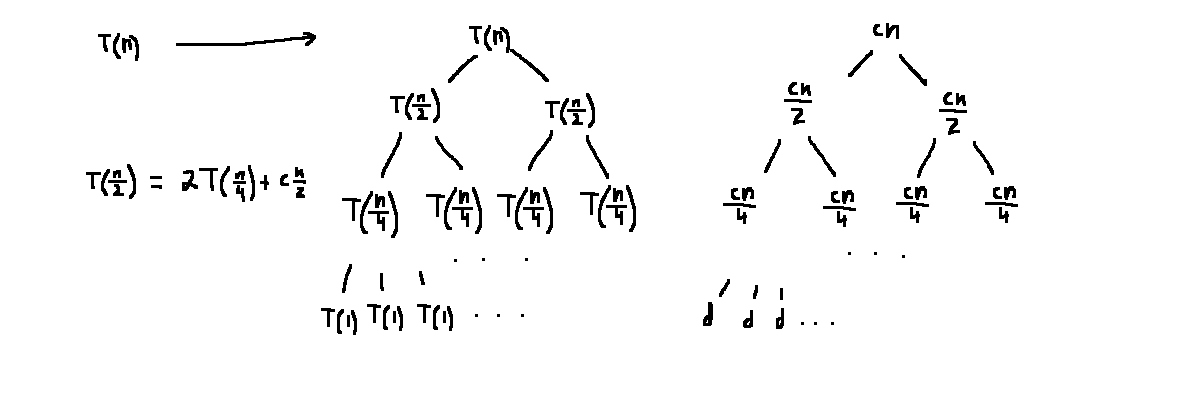
Row \(i\) has \(2^i\) nodes with value \(\frac{cn}{2^i}\).

Given \(n=2^j\) for some \(j\), the tree wil have \(j\) rows.

\[\begin{align*} \text{Total} &= j(c) + d2^j\\ &= (\log_{2} n)c + dn \end{align*}\]

Master theorem

For a recurrence relation in the form:

\[T(n) = aT\left(\frac{n}{b}\right) + \Theta(n^y), \quad a\ge 1, b \gt 1\]

Where \(n\) is a power of \(b\). Define \(x=\log_b{a}\). Then:

\[T(n) \in \begin{cases} \Theta(n^x), &y \lt x\\ \Theta(n^x \log n), &y = x\\ \Theta(n^y), &y \gt x\\ \end{cases}\]

Modified general version

For a recurrence relation in the form:

\[T(n) = aT\left(\frac{n}{b}\right) + f(n)\]

Where \(n\) is a power of \(b\). Define \(x=\log_b{a}\). Then:

\[T(n) \in \begin{cases} \Theta(n^x), &\exists \epsilon \gt 0 \mid f(n) \in O(n^{x-\epsilon})\\ \Theta(n^x \log n), &f(n) \in \Theta(n^x)\\ \Theta(f(n)), &\exists \epsilon > 0 \mid \frac{f(n)}{n^{x+\epsilon}} \text{ is increasing }\\ \end{cases}\]

e.g.

\[T(n) = 3T\left(\frac{n}{4}\right) + n\log n\]

\[\begin{align*} x &= \log_b a\\ &= \log_4 3\\ &\approx 0.793\\ \\ \text{Let } \epsilon &= 0.1\\ \\ \frac{f(n)}{n^{x+\epsilon}} &= \frac{n^1 \log n}{n^{0.793+\epsilon}}\\ &= \frac{n^1 \log n}{n^{0.893}}\\ \text{This is an increasing function,} &\therefore \text{ case 3 applies }\\ &\Rightarrow T(n) \in \Theta(n\log(n))\\ \end{align*}\]