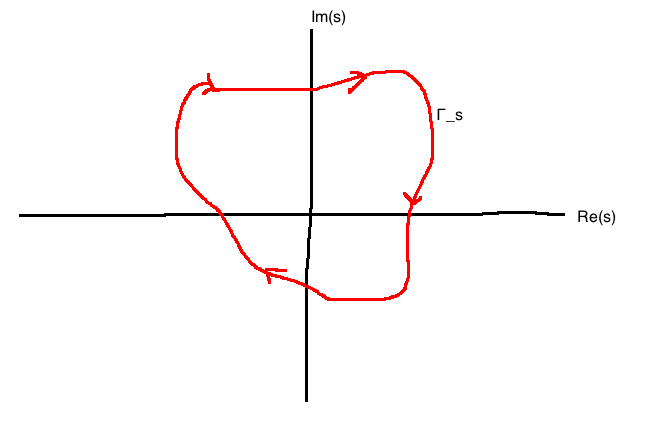
Consider a closed curve in the \(s\)-plane with no self-intersections and with negative (clockwise) orientation.

Now let \(G(s) \in \mathbb{R}(s)\). For each \(s \in \mathbb{C}\), \(G(s)\) is another complex number, so \(G: \mathbb{C} \rightarrow \mathbb{C}\)
If \(\Gamma_s\) doesn't pass through any poles of \(G\), then as \(s\) makes a circuit around \(\Gamma_s\), \(G(s)\) traces out a different closed curve that we'll call \(\Gamma_G\).
\[G(s) = s-1\]
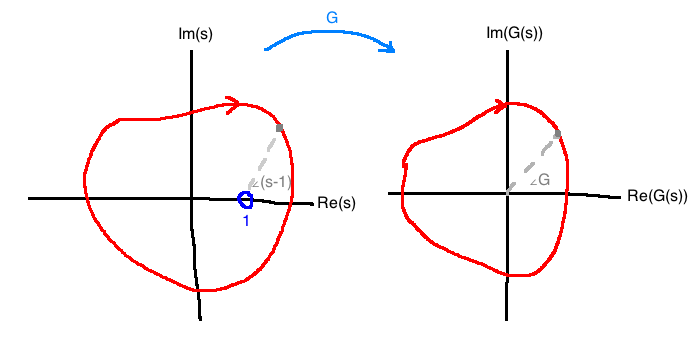
Since \(\Gamma_s\) encircles a zero of \(G\), the angle of \(G\) will change by \(-2\pi\) as \(s\) makes a circuit around \(\Gamma_s\).
\[G(s) = s-1\]
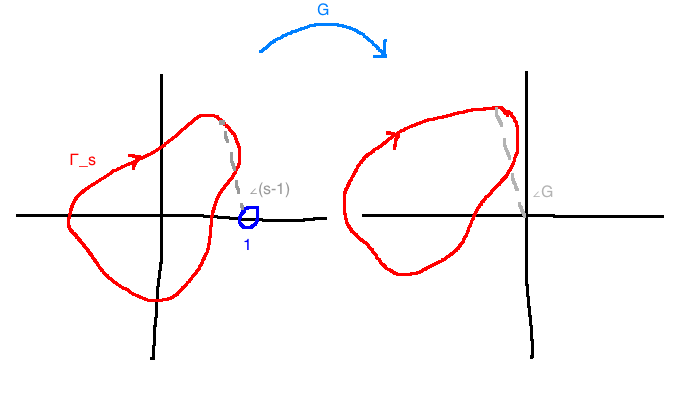
Now the net change in \(\angle G(s)= \angle(s-1)\) as \(s\) moves around \(\Gamma_s\) is zero. This means that \(\Gamma_G\) does not encircle the origin.
\[G(s) = \frac{1}{s-1}\]

\(\angle(s-a) = -\angle G\) because the pole is in the denominator.
Now, \(\angle (s-1)\) changes by \(-(-2\pi)=2\pi\) as the point makes a circuit aorund \(\Gamma_s\). Therefore, \(\Gamma_G\) must have a net angular change of \(2\pi\) as \(s\) moves around \(\Gamma_s\). \(\Gamma_G\) must encircle the origin once.
Suppose \(G(s) \in \mathbb{R}(s)\) has no poles or zeroes on \(\Gamma_s\), but \(\Gamma_s\) encircles \(n\) poles of \(G\) and \(m\) zeroes of \(G\). Then, \(\Gamma_g\) has \(n-m\) counter-clockwise encirclements of the origin.
Write \(G\) like so:
\[G(s) = K \frac{\prod_i (s-z_i)}{\prod_i (s - p_i)}\]
\(K\) is a real gain, \(z_i\) are zeroes, and \(p_i\) are poles. Then, for each \(s\) on \(\Gamma_s\):
\[\angle G(s) = \angle K + \sum \angle(s-z_i) - \sum \angle (s-p_i)\]
If the zero \(z_i\) is enclosed by \(\Gamma_s\), the net change in the term \(\angle(s-z_i)\) after one circuit around \(\Gamma_s\) is \(-2\pi\). If \(z_i\) isn't enclosed, the net change is zero.
So, the net change in \(\angle G\) is \(m(-2\pi) - n(-2\pi) = (n-m)2\pi\).
\(\Gamma_G\) must encircle the origin \(n-m\) times in the counterclockwise direction.

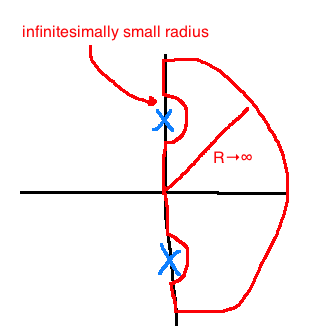
Take \(\Gamma_s\) to encircle the whole right-half plane
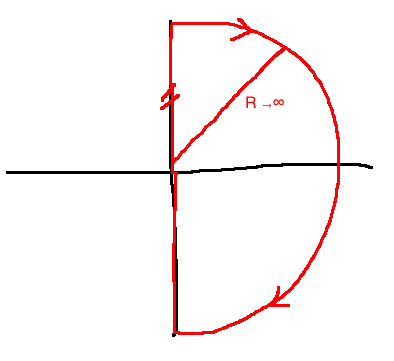
For this choice of \(\Gamma_S\), the corresponding curve \(\Gamma_G\) is called the Nyquist plot of \(G\). If \(G\) has no poles or zeroes on \(\Gamma_s\), then by the principle of the argument, the Nyquist plot will encircle the origin \(n-m\) times in counterclockwise direction.
\(n\) is the number of poles of \(G\) with \(\Re(s) \gt 0\), \(m\) is the number of zeroes of \(G\) with \(\Re(s) \gt 0\).
If \(G\) has poles on \(j\mathbb{R}\), we'll indent around them.
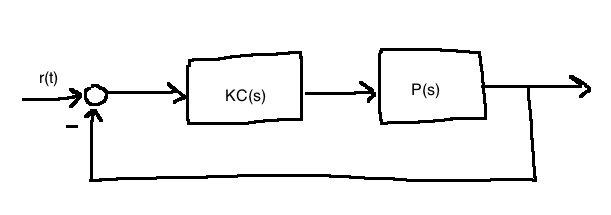
Assuming \(C,P\) are rational:
Key idea: if the system is IO stable, then the poles of \(\frac{Y(s)}{R(s)} = \frac{KC(s)P(s)}{1+KC(s)P(s)}\) must all be in \(\mathbb{C}^-\). So, we'll work with the transfer function \(G(s)=1+KC(s)P(s)\).
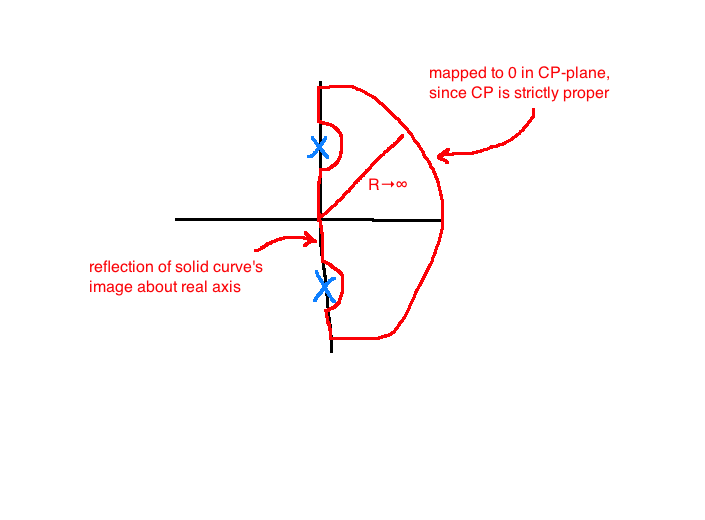
Let \(n\) denote the number of poles of \(C(s)P(s)\) in \(\mathbb{C}^+\). Construct the Nyquist plot of \(C(s)P(s)\) indenting to the right around any poles on the imaginary axis. The feedback system is IO stable if and only if the Nyquist plot doesn't pass through \(\frac{-1}{K}\) and encircles \(\frac{-1}{K}\) exactly \(n\) times counterclockwise.
\[\frac{Y(s)}{R(s)} = \frac{KC(s)P(s)}{G(s)}\]
Since we've assumed no unstable pole-zero cancellations, IO stability is equivalent to \(G(s)\) having no zeroes with \(\Re(s) \ge 0\). (See Theorem 5.2.10.)
I.O. stability \(\Leftrightarrow \frac{KC(s)P(s)}{G(s)}\) has no poles with \(\Re(s) \ge 0 \Leftrightarrow G(s)\) has no zeroes with \(\Re(s) \ge 0\).
Since \(G(s)=1+K\frac{N_c(s)}{D_c(s)} \frac{N_p(s)}{D_p(s)} = \frac{D_cD_p+KN_cN_p}{D_cD_p}\), so \(G\) has the same poles as \(CP\). Therefore, \(G\) has \(n\) poles with \(\Re(s) \gt 0\).
Since \(\Gamma_s\) indents around poles on \(j\mathbb{R}\) and since \(G\) is proper, \(\Gamma_s\) doesn't pass through any poles of \(G\). By the principle of the argument, \(\Gamma_G\) will encircle the origin \(n-m\) times in the counterclockwise direction.
Since we need no zeroes with \(\Re(s) \gt 0\), we need \(m=0\) for stability. Since \(C(s)P(s) = \frac{1}{K}G(s) - \frac{1}{K}\), the Nyquist plot of \(CP\) is going to be the Nyquist plot of \(G\) scaled (possibly by \(K\)) and then shifted to the left by \(\frac{-1}{K}\).
Conclusion: IO stability exists if and only if the Nyquist plot of \(CP\) encircles \(\frac{-1}{K}\) \(n\) times in the counterclockwise direction.
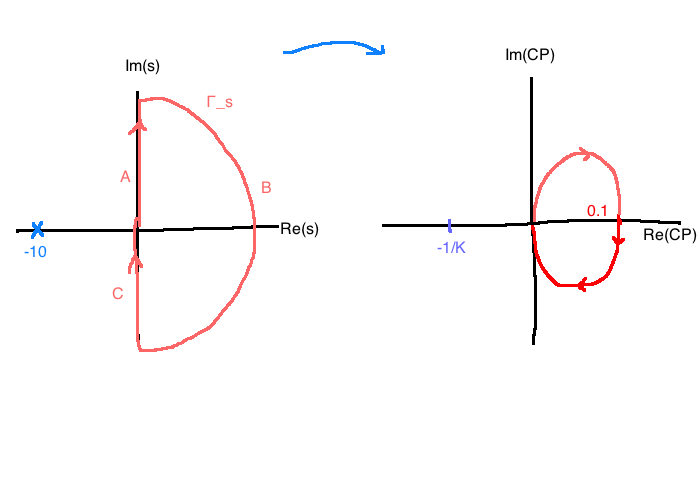
Since \(C(s)P(s)\) is rational, we have:
Expect a question on the final asking to apply this
\[C(s)P(s)=\frac{1}{s+10}\]
We can also test for other values of \(K\):
| \(\frac{-1}{K} \in (-\infty, 0)\) | \(\frac{-1}{K} \in [0, 0.1]\) | \(\frac{-1}{K} \gt 0.1\) | |
|---|---|---|---|
| \(N\) | 0 | -1 | 0 |
This implies it is stable for \(K \gt -10\).
\[C(s)P(s) = \frac{1}{s+10}\]
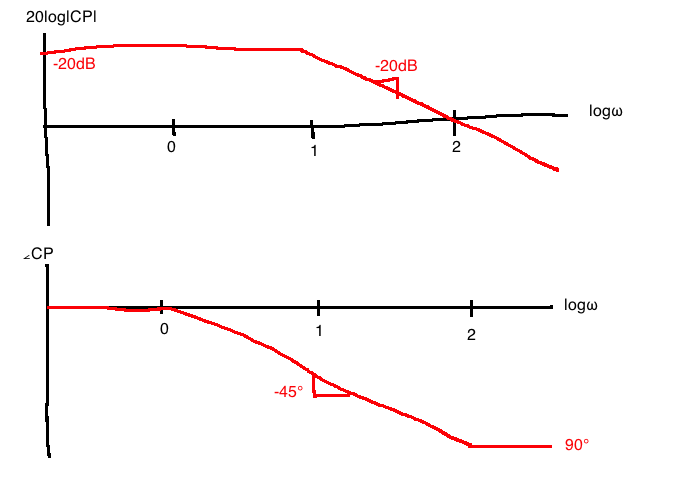
\[C(s)P(s) = \frac{s+1}{s(s-1)}\]

Segment A:
Segment B:
Segment C:
Segment D:
Observe the number of counterclockwise encirclements of \(\frac{-1}{K}\):
| \(-\infty \lt \frac{-1}{K} \lt -1\) | \(-1 \lt \frac{-1}{K} \lt 0\) | \(0 \lt \frac{-1}{K} \lt \infty\) | |
|---|---|---|---|
| \(N\) | -1 | +1 | 0 |
Since we have \(n=1\), we need \(N=1\) for input-output stability. Therefore, \(K \gt 1\).
If a system is stable, how stable?
Nominal model: \(\phi=0\), input-output stability
How much phase change \(\phi\) can I tolerate before losing IO stability? Recall that \(|e^{j\phi}|=1\), \(\angle e^{j\phi}=\phi\)
\[L(s) = \frac{1}{(s+1)^2}\]
\(n=0\), so we need zero counterclockwise encirclements of -1 to get IO stability.


Nominal design: \(K=1\), IO stable. How much gain can we change \(K\) by before we lose stability?
\[ L(s)=\frac{2}{(s+1)^2\left(\frac{s}{10}+1\right)}\]
\(n=0\) (no open-loop unstable poles), so we need \(N=0\) counterclockwise encirclements of -1 for IO stability.

From the Nyquist criterion, the nominal model is IO stable. The system remains stable so long as \(\frac{-1}{K} \lt \frac{-1}{12.1}\). This means we can increase \(K\) up to 12.1 before losing stability. This value of \(K\) is called the gain margin.

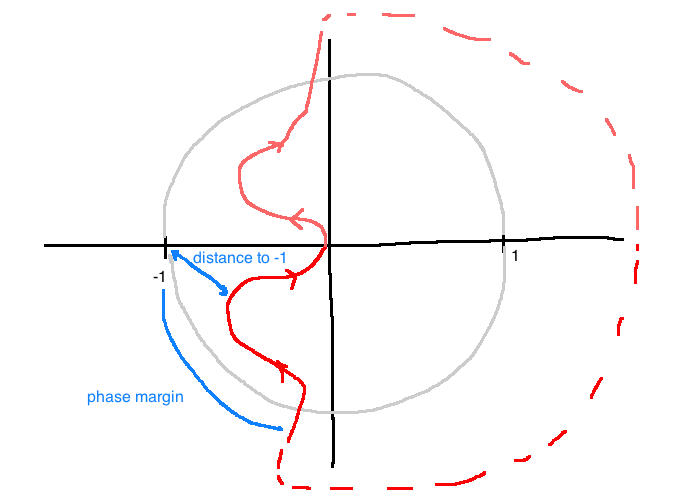
Phase margin is related to the distance on the Nyquist plot from to -1, measured as a rotation along the unit circle.
Gain margin is the distance on the Nyquist plot to -1 along the real axis.
More generally, we'll want to use the Euclidean distance from the Nyquist plot to -1 as a measure of stability.
\[L(s) = \frac{0.38(s^2+0.1s+0.55)}{s(s+1)(s^2+0.06s+0.5)}\]
\(n=0\) so we need \(N=0\) counterclockwise encirclements of -1.
Consider for a moment our normal feedback system with no disturbances. The transfer function from \(r\) to \(e\):
\[\frac{E(s)}{R(s)} = \frac{1}{1+P(s)C(s)} =: S(s)\]
Assume IO stability. Then the distance from \(L=CP\) to -1 is:
\[\begin{align}
\min_\omega \left|-1-L(j\omega)\right| &= \min_\omega \left|-1-CP\right|\\
&= \left(\max_\omega \left|\frac{1}{1+CP}\right|\right)^{-1}\\
&= \left(\max_\omega \left|S(j\omega)\right|\right)^{-1}\\
\end{align}\]
So, the distance from the Nyquist plot to -1 is the reciprocal of the peak magnitude of the Bode plot of \(S\). We'll call this \(S_m\), for stability margin.