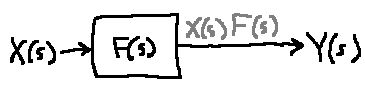
Square blocks multiply. In this case, \(Y(s) = X(s)F(s)\).
Things I think are important to understanding the prelab
If \(f(t)\) is a function in the time domain, then the laplace transform \(\mathcal{L}\{f(t)\} = F(s)\) is in the frequency domain.
\(s\) is a complex variable, so \(s = \sigma_{\text{(real part)}} + j\omega_{\text{(imaginary part)}}\).
Transfer functions exist in the \(s\)-plane, not the time plane.
The transfer function \(T(s)\) of a system with an input signal \(X(s)\) and output \(Y(s)\) is just defined to be the ratio of output to input:
\[T(s) = \frac{Y_{\text{(output)}}(s)}{X_{\text{(input)}}(s)}\]
A pole is an asymptote in the transfer function.
There is a direct mapping from block diagram to transfer function:

Square blocks multiply. In this case, \(Y(s) = X(s)F(s)\).
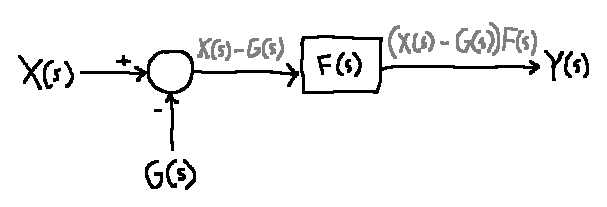
Circle blocks sum, taking into account signs on input arrows. In this case, \(Y(s) = (X(s)-G(s))F(s)\).
You can produce an input \(x(t)\) and measure the system response \(y(t)\). Then, you can just take the Laplace transform of \(x(t)\) and divide it by the Laplace transform of \(y(t)\) to get the transfer function.
You gave a unit step as an input to a system and got a response \(y(t)\). The time constant \(\tau\) is just the \(t\) value that decays the unit step response to either \(1 - \frac{1}{e}\) times its final value if the function is increasing, or \(\frac{1}{e}\) times its final value if it is decreasing.
For example, imagine the response is \(y(t) = 20e^{-5 t}\):
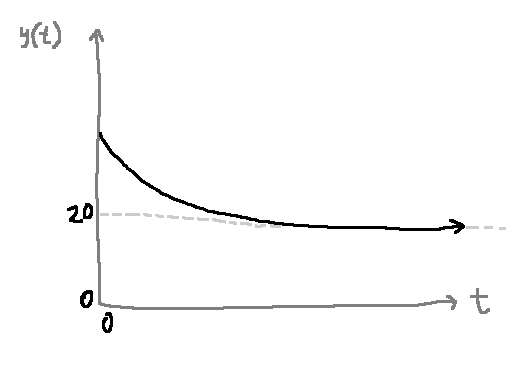
The function decreases to its final value 20, so the time constant is the \(t\) where its value is \(\frac{20}{e}\):
\[\begin{align} f(\tau) &= \frac{20}{e}\\ &= 20e^{-1}\\ 20e^{-1} &= 20e^{-5 \tau}\\ e^{-1} &= e^{-5 \tau}\\ -1 &= -5 \tau\\ \tau = \frac{1}{5} \end{align}\]
Given a transfer function \(T(s)\), the gain of frequency \(\omega\) is defined as \(\left| T(j \omega) \right|\).
\(\omega\) is a frequency in rad/s, so you can put any frequency value in there as input instead of using a variable. Remember as well that \(|j|=1\).